转摘【深度学习】生成对抗网络Generative Adversarial Nets
序言
本文是GAN网络的原始论文,发表于2014年,我们知道,对抗网络是深度学习中,CNN基础上的一大进步; 它最大的好处是,让网络摆脱训练成"死模型"到固定场所处去应用,而是对于变化的场景,网络有一个自己的策略; 这是非常值得研究的课题。 本文记录了原始论文,作为长期参考系保存。
一、摘要
我们提出了一个通过对抗过程估计生成模型的新框架,其中我们同时训练两个模型:捕获数据分布的生成模型G,以及估计样本来自训练数据而不是G的概率的判别模型D。 G 的训练过程是最大化 D 出错的概率。 此框架对应于最小最大值双人游戏。 在任意函数 G 和 D 的空间中,存在一个唯一的解决方案,G 恢复训练数据分布,D 在任何地方都等于 1 2。 在G和D由多层感知器定义的情况下,整个系统可以通过反向传播进行训练。 在训练或生成样本期间,不需要任何马尔可夫链或展开的近似推理网络工作。 实验通过对生成的样本进行定性和定量评估,证明了该框架的潜力。
二、概述
深度学习的前景是发现丰富的分层模型[2],这些模型表示人工智能应用中遇到的各种数据的概率分布,例如自然图像,包含语音的音频波形和自然语言语料库中的符号。 到目前为止,深度学习中最引人注目的成功涉及判别模型,通常是那些将高维、丰富的感官输入映射到类标签的模型[14,22]。 这些惊人的成功主要基于反向传播和辍学算法,使用分段线性单元[19,9,10],这些单元具有特别好的梯度。 深度生成模型的影响较小,因为难以近似最大似然估计和相关策略中出现的许多棘手的概率计算,并且由于难以在生成上下文中利用分段线性单元的优势。 我们提出了一种新的生成模型估计程序,可以避开这些困难。 1 在提议的对抗网络框架中,生成模型与对手对抗:一种区分模型,它学习确定样本是来自模型分布还是数据分布。 生成模型可以被认为是类似于一队造假者,试图生产假币并在不被发现的情况下使用它,而歧视模型类似于警察,试图检测假币。 这场游戏的竞争促使两支球队改进他们的方法,直到假冒产品与真品密不可分
该框架可以为多种模型和优化算法生成特定的训练算法。 在本文中,我们探讨了生成模型通过将随机噪声传递到多层感知器来生成样本的特殊情况,并且判别模型也是多层感知器。 我们将这种特殊情况称为对抗性网络。 在这种情况下,我们可以仅使用非常成功的反向传播和 dropout 算法 [17] 来训练这两个模型,并仅使用前向传播从生成模型中抽样。 不需要近似推理或马尔可夫链。
三、相关工作
具有潜在变量的有向图模型的替代方案是具有潜在变量的无向图模型,例如受限玻尔兹曼机(RBM)[27,16],深度玻尔兹曼机(DBM)[26]及其众多变体。 这些模型中的交互作用表示为非规范化势函数的乘积,通过随机变量所有状态的全局求和/积分进行归一化。 这个量(分割函数)及其梯度对于除了最微不足道的实例之外的所有实例都是难以处理的,尽管它们可以通过马尔可夫链蒙特卡罗(MCMC)方法估计。 混合给依赖MCMC的学习算法带来了一个重大问题[3,5]。 深度置信网络(DBN)[16]是包含单个无向层和sev有向层的混合模型。 虽然存在快速近似逐层训练标准,但 DBN 会产生与无向和有向模型相关的计算困难。 还提出了不近似或限制对数似然的替代标准,例如分数匹配[18]和噪声对比估计(NCE)[13]。 这两者都需要通过分析指定学习的概率密度,直至归一化常数。 请注意,在许多具有多层潜在变量(例如 DBN 和 DBM)的有趣生成模型中,甚至不可能推导出可处理的非规范化概率密度。 一些模型,如去噪自动编码器[30]和收缩自动编码器,其学习规则与应用于RBM的分数匹配非常相似。 在 CHE 中,与这项工作一样,采用判别性训练标准来适应生成模型。 然而,生成模型本身不是拟合单独的判别模型,而是用于区分生成的数据与固定噪声分布的样本。 由于 NCE使用固定噪声分布,因此在模型在观察到的变量的一小部分上学习到甚至大致正确的分布后,学习速度会大大减慢。 最后,一些技术不涉及显式定义概率分布,而是训练生成机器从所需的分布中提取样本。 这种方法的优点是可以将此类机器设计为通过反向传播进行训练。 该领域最近的突出工作包括生成随机网络(GSN)框架[5],它扩展了广义去噪自动编码器[4]:两者都可以被视为定义参数化马尔可夫链,即学习执行生成马尔可夫链一步的机器的参数。 与GSN相比,对抗网络框架不需要马尔可夫链进行采样。 由于对抗网络在生成过程中不需要反馈环路,因此它们能够更好地利用分段线性单元[19,9,10],这提高了反向传播的性能,但在反馈循环中使用时存在无限激活的问题。 通过反向传播来训练生成机器的最新示例包括最近关于自动编码变分贝叶斯 [20] 和随机反向传播 [24] 的工作。
四 对抗网络
当模型都是多层感知器时,对抗建模框架最直接应用。 为了学习生成器在数据 x 上的分布 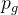,我们在输入噪声变量 ) 上定义一个先验,然后将到数据空间的映射表示为),其中 G 是由参数为  的多层感知器表示的可微函数。 我们还定义了第二个多层感知器 ),它输出单个标量。 D(x) 表示 x 来自数据而不是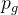 的概率。 我们训练 D 以最大限度地提高为训练样本和来自 G 的样本分配正确标签的概率。 我们同时训练 G 以最小化对数
)));
)玩两个极限minimax; 换句话说,D和G两个玩家; 它们针对数值函数。
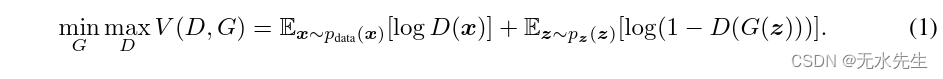
在下一节中,我们提出了对抗网络的理论分析,本质上表明训练标准允许一个恢复数据生成分布作为GandDaregiven足够的容量,即非参数限制。见图1方法的无正式性,更教学性的解释。在实践中,我们必须使用迭代的、数值的方法来实现游戏。优化Dtocompleteininnerloopoftraining是计算禁止的,andonfinitedatasets将导致过度拟合。相反,wealternateateinterweenkstepsofoptimization DandonestepofoptimizingG.thisresultsinDbeingmaintainnearitsoptimalsolution,所以只要Gchangesslowlylyly.thisstrategy类似于SML/PCD[31,29]训练维护样本从aMarkovchainfromonelearningsteptothenextinto避免燃烧inaMarkovchainaspartoftheinnerloopoflearning.Theprocedureisformally presentlyin Algorithm1.
完成一步优化 G。 这导致 D 保持在其最佳解附近,所以只要变化足够慢。 该策略与SML/PCD[31,29] 的方式类似训练维护马尔可夫链中的样本,从一个学习步骤到下一个学习步骤,以避免燃烧马尔可夫链作为学习内循环的一部分。 该程序被正式提出在算法1中。
在实践中,方程1可能无法为G学习提供足够的梯度。在早期学习中,当 Gispoor 时,D 可以高度自信地拒绝样本,因为它们明显不同于训练数据。在这种情况下,log(1 D(G(z))) 饱和。而不是训练 G 最小化log(1 D(G(z)))我们可以训练G来最大化logD(G(z))。这个目标函数的结果是G 和 D 的动力学相同的固定点,但在学习早期提供更强的梯度。
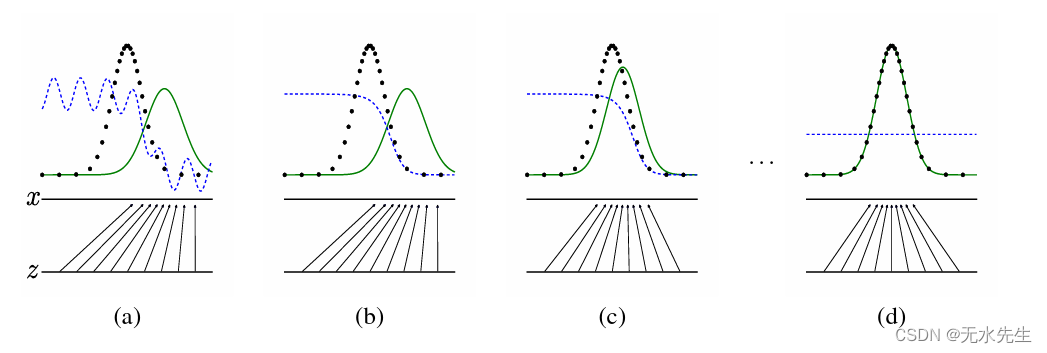
图1:生成对抗网络是通过同时更新判别分布来训练的 (D,蓝色,虚线)以便区分来自数据生成分布的样本(黑色, 虚线)px来自那些生成分布pg(G)(绿色,实线)。下水平线是 z 从中采样的域,在本例中是均匀采样的。上面的水平线是域的一部分 x 的向上箭头显示映射 x=G(z) 如何施加非均匀分布 pgon 变换后的样本。高密度区域中的 G 收缩和 pg 流密度区域中的扩展。(a) 考虑接近收敛的对抗对:pg 是相似的顶级数据和不同准确的分类器。 (b) 在算法的内循环中,训练从数据中区分样本,收敛到 D(x)= pdata(x) pdata(x)+pg(x) (c)更新G后,D的梯度引导G(z)流向更有可能的区域 (d)经过几个步骤的训练,如果G和D有足够的容量,他们将达到 两者都无法改进,因为 pg=pdata。鉴别器无法区分 两个分布,即 D(x)=1 2 。
五、理论结果
生成器隐式定义概率分布 pgas 样本的分布 G(z)当z pz时获得。因此,我们希望算法1收敛到好的估计器
pdata,如果有足够的容量和训练时间。本节的结果是在参数设置,例如通过研究收敛性来表示无限容量的模型 概率密度函数空间。
我们将在第 4.1 节中展示,这个 minimax 游戏具有 pg=pdata 的全局最优值。我们将 然后在第 4.2 节中显示算法 1 优化了方程 1,从而获得了期望的结果。

5.1  的全局最优性
我们首先考虑任意给定生成器 G 的最佳判别器 D。
命题1.对于G固定后,最优判别器D是

=\frac{P_{data}(x)}{P_{data}(x)+P_g(x)})
证明.判别器 D 的训练标准,给定任何生成器 G,都会最大化数量)
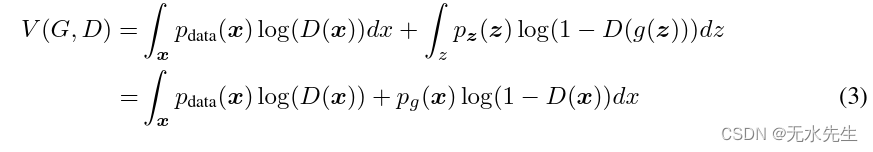
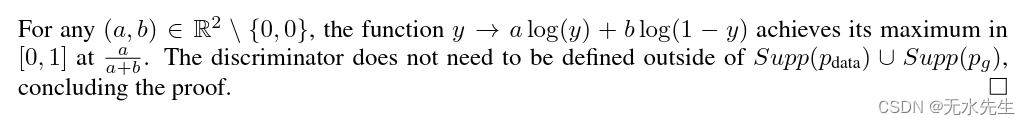
对任意\in \mathbb R^2 \setminus (0,0)),那函数 + blog(1-y))在取最大的时候,落在![[0,1]](https://latex.csdn.net/eq?[0,1])上,鉴别器不需要在\cup Supper(P_{g}))外部定义.
请注意,D 的训练目标可以解释为最大化对数似然计时条件概率),其中Y表示x是否来自 (with y=1)或来自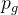(with y=0)。方程1中的最小最大博弈现在可以重新表述为:
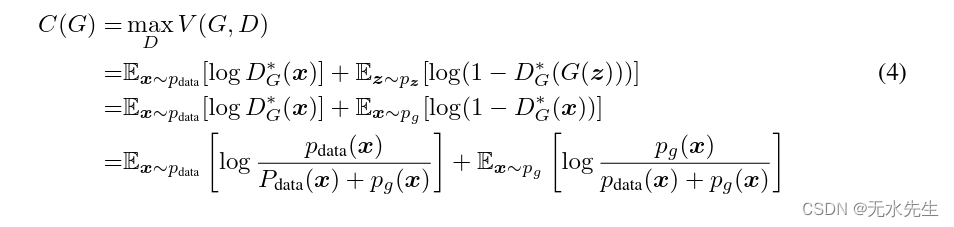
定理 1. 虚拟训练标准 C(G) 的全局最小值达到当且仅当.此时,C(G) 达到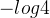 值。
【证明】对于, = 1 /2),(考虑等式2)。因此,通过检查等式4 在  = 1/2)、我们 F 指数  = log 1/2 +log 1/2 =-log4)。看到这是 C(G) 的最佳可能值,达到 仅对于,观察到

通过从 = V (D^*_G,G)) 中减去该表达式,我们得到:
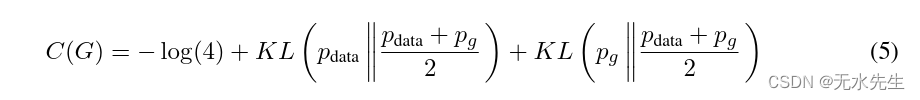
其中 KL 是 Kullback-Leibler 散度。我们在前面的表达式中认识到 Jensen模型分布与数据生成过程之间的香农散度:

由于两个分布之间的 Jensen-Shannon 散度始终为非负且为零 仅当它们相等时,我们才证明 )是 ) 的全局最小值,并且 唯一的解决方案是 ,即生成模型完美地复制数据生成 过程.
5.2 算法1的收敛性(Convergence of Algorithm1)
命题2.如果G和D有足够的容量,并且在算法1的每一步,判别器 允许达到给定G的最优值,并且更新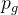以改进标准 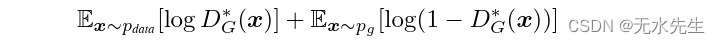
那么: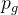收敛到
【证明】将 = U(p_g,D))视为 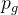 的函数,如上述标准中所做的那样。笔记 )在 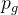 中是凸的。凸函数的上界的导数包括 函数在达到最大值时的导数。换句话说,如果 = sup_{\alpha \in A}f_\alpha (x))和 ) 对于每个α ,在 x 中是凸的,则如果), \in \partial f)。 这相当于在给定相应 G 的情况下,在最优 D 处计算 pg 的梯度下降更新。)在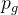 中是凸的,具有唯一的全局最优值,如 Thm 1 中所证明的, 因此,通过足够小的 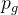 更新,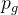 收敛于 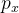,从而得出证明.
在实践中,对抗性网络通过函数 )表示有限的 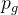 分布族, 我们优化  而不是 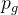 本身。使用多层感知器定义 G 引入 参数空间中的多个临界点。然而,多层板的优异性能 实践中的感知器表明,尽管缺乏理论依据,但它们是一个合理的模型 保证。
六、实验
我们训练的对抗网络包括一系列数据集,包括 MNIST[23]、多伦多人脸数据库(TFD) [28] 和 CIFAR-10 [21]。发电机网络使用整流器线性激活的混合[19,9] 和 sigmoid 激活,而判别器网络使用 maxout [10] 激活。辍学 [17]应用于训练鉴别器网络。虽然我们的理论框架允许使用生成器中间层的丢失和其他噪声,我们仅使用噪声作为输入生成器网络的最底层。
我们通过将高斯 Parzen 窗口拟合到 G 生成的样本并报告该分布下的对数似然来估计 pg 下测试集数据的概率。参数
高斯分布是通过验证集上的交叉验证获得的。 Breuleux 等人介绍了该程序。 [8] 并用于各种生成模型,其确切的可能性难以处理 [25,3,5]。结果如表 1 所示。这种估计可能性的方法具有较高的方差,并且在高维空间中表现不佳,但它是据我们所知可用的最佳方法。可以采样但不能估计可能性的生成模型的进步直接激发了对如何评估此类模型的进一步研究。
 表 1:基于 Parzen 窗口的对数似然估计。 MNIST 上报告的数字是平均对数测试集上样本的可能性,以及跨示例计算的平均值的标准误差。在 TFD 上,我们 计算数据集折叠的标准误差,并使用验证集选择不同的标准误差 每一次折叠。在 TFD 上,对每个折叠进行交叉验证,并计算每个折叠的平均对数似然。 对于 MNIST,我们与数据集实值(而不是二进制)版本的其他模型进行比较。
在图 2 和图 3 中,我们显示了训练后从生成器网络中抽取的样本。虽然我们不做 声称这些样本比现有方法生成的样本更好,我们相信这些样本 样本至少与文献中更好的生成模型具有竞争力,并强调 对抗性框架的潜力。

图 2:模型样本的可视化。最右边的列显示了最近的训练示例 邻近样本,以证明模型没有记住训练集。样品 是公平随机抽取的,而不是精心挑选的。与深度生成模型的大多数其他可视化不同,这些 图像显示模型分布中的实际样本,而不是给定隐藏单元样本的条件均值。 而且,这些样本是不相关的,因为采样过程不依赖于马尔可夫链 混合。 a) MNIST b) TFD c) CIFAR-10(全连接模型) d) CIFAR-10(卷积判别器) 和"反卷积"生成器)
七、优点和缺
相对于以前的建模框架,这个新框架有优点和缺点作品。缺点主要是没有 pg(x) 的显式表示,并且 D训练时必须与G保持良好的同步(特别是G不能训练太多)不更新 D,以避免"Helvetica 场景",其中 G 折叠太多值z 的值与 x 的值相同,以具有足够的多样性来建模 pdata),就像 a 的负链一样玻尔兹曼机必须在学习步骤之间保持最新状态。优点是马尔可夫永远不需要链,仅使用反向传播来获取梯度,期间不需要推理学习,并且可以将多种功能合并到模型中。表 2 总结
生成对抗网络与其他生成建模方法的比较。
上述优点主要是计算上的。对抗模型也可能获得收益生成器网络的一些统计优势未通过数据检查直接更新ples,但仅限于梯度流经鉴别器。这意味着该组件的输入不会直接复制到生成器的参数中。对抗网络的另一个优点其工作原理是它们可以表示非常尖锐的、甚至是退化的分布,而基于马尔可夫链要求分布有些模糊,以便链能够模式之间的混合
参考原文:
[1406.2661.pdf (arxiv.org)](https://arxiv.org/pdf/1406.2661.pdf "1406.2661.pdf (arxiv.org)")
===========================
【来源: CSDN】
【作者: 无水先生】
【原文链接】 https://yamagota.blog.csdn.net/article/details/131992590
声明:转载此文是出于传递更多信息之目的。若有来源标注错误或侵犯了您的合法权益,请作者持权属证明与本网联系,我们将及时更正、删除,谢谢。