转摘【基础理论】介绍一个概率分布:柯西分布
目录
一、提要
连续概率密度函数究竟有多少,应该有无穷多。在诸多分布函数中,高斯分布可能是最著名的。然而,有没有类似于高斯函数的分布,而形式上不是指数函数的呢?回答是有,柯西分布就是一种。
二、柯西分布的几何解释
柯西分布,也称为柯西-洛伦兹分布或洛伦兹分布,是描述共振行为的连续分布。它还描述了以随机角度倾斜的线段切割 x 轴的水平距离分布。如图:我们从原点引出射线,相邻射线角度相等,这些射线与平行于x轴的直线S有交点,这些交点在S线上的密度是不同的,显然,在90°的附近密度最大。(目测)
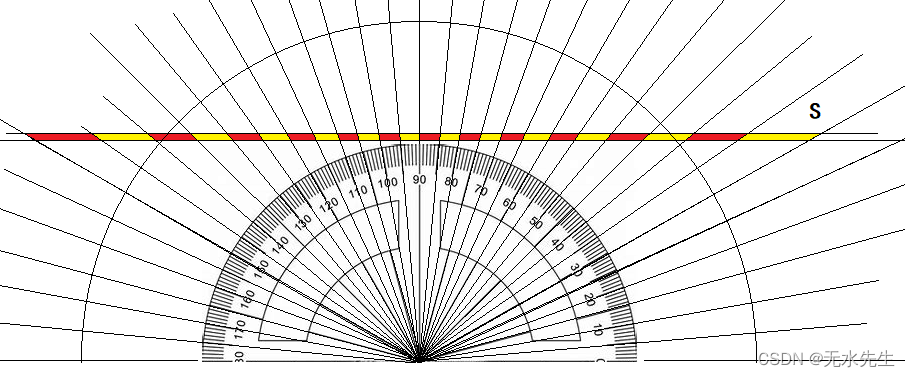
[Cauchy Distribution -- from Wolfram MathWorld](https://mathworld.wolfram.com/CauchyDistribution.html "Cauchy Distribution -- from Wolfram MathWorld")
让 θ 表示具有固定旋转点的线与垂直轴所成的角度,如图所示。然后
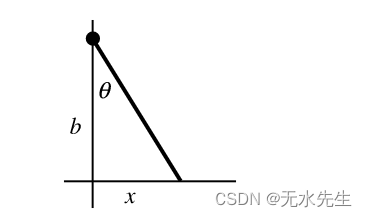
 (1)
 (2)
 (3)
 (4)
将(4)分别取积分:

显然,左边是对![\[-\frac{\pi}{2},\frac{\pi}{2}]](https://latex.csdn.net/eq?\[-\frac{\pi}{2},\frac{\pi}{2}])上均匀分布积分,后者是对某个函数在整个数轴积分,两个都是1;显然都能构成概率密度函数。(注意概率密度函数的三个要素)
后者的概率密度函数就是柯西分布。即:
 = \frac{1}{ \pi } \frac{b }{b^2+x^2})
更一般的写法是:
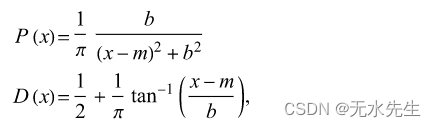
密度函数和分布函数的曲线:
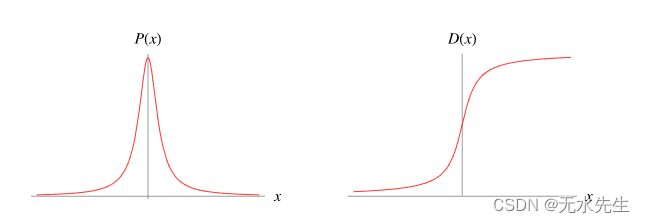
其中 b 是半峰半宽,m 是统计中位数。在关于的图示中,m=0。Cauchy 分布在 Wolfram 语言中实现为 CauchyDistribution[m, Gamma/2].
三、性质
柯西分布的均值、方差都不存在!。下面我们使用[numpy](https://so.csdn.net/so/search?q=numpy&spm=1001.2101.3001.7020 "numpy")对它进行抽样,并和标准正态分布进行对照。
python
import numpy as np
from matplotlib import pyplot as plt
cnt=1000 #抽样1000个样本点
x=np.random.standard_cauchy(cnt)
y=np.random.randn(cnt)
plt.figure()
plt.subplot(2,1,1)
plt.hist(x,100,density=True)
plt.legend(['Cauchy'])
plt.subplot(2,1,2)
plt.hist(y,100,density=True)
plt.legend(['Gauss'])
plt.show()结果图:
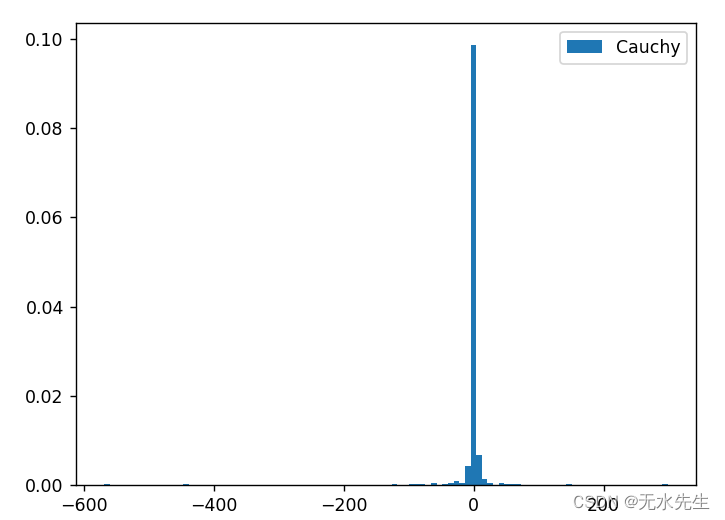
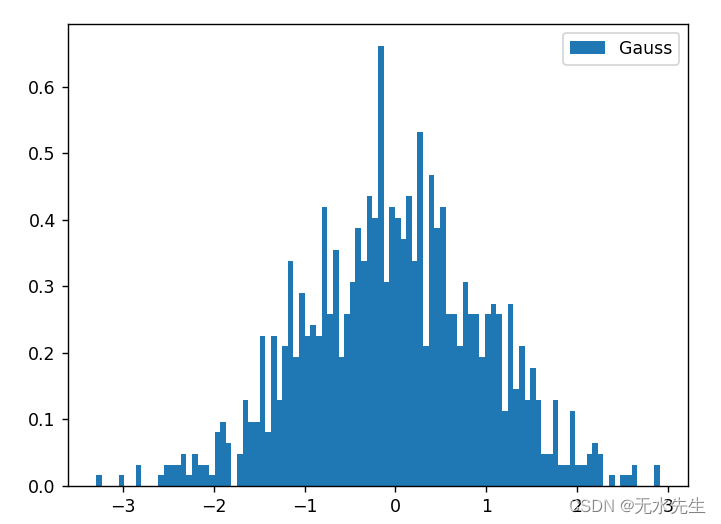
四、结论
柯西分布的取值范围非常广,很大的值也有一定概率取到,因而柯西分布也称为heavy-tail distribution。并且相比于gaussian,概率密度的最大取值只有0.1,就是x=0的那个地方。
而高斯分布的取值就集中很多,0处的概率密度为0.6左右。
再有,在量子世界,粒子和粒子距离很远,比如,电子到原子核的距离,就好比一个汽车到三千公里外的一个城市距离,因此,要显著描述电子的位置分布,只能是柯西-洛伦兹分布,不能用高斯分布刻画,因为高斯分布尺度不够,信号太弱,噪声将把电子的电磁能量淹没,模型无效。
===========================
【来源: CSDN】
【作者: 无水先生】
【原文链接】 https://yamagota.blog.csdn.net/article/details/126877539
声明:转载此文是出于传递更多信息之目的。若有来源标注错误或侵犯了您的合法权益,请作者持权属证明与本网联系,我们将及时更正、删除,谢谢。